Hallo liebe leute,
Legende:
N = Modul,
e = Verschlüsselungsexponent,
p, = die erste Primzahl,
q = die zweite Primzahl,
Ich habe mir gerade zur Aufgabe gemacht den RSA Algorithmus nachzuprogrammieren. Beim RSA handelt es sich um ein asymmetrisches Kryptosystem. Dies beudetet, dass es immer ein public + privatekey geben muss.
Also:
N = p * q ist , bzw phi(n) = (p-1) * (q-1)
Um N zu berechnen habe ich nun einen primzahlenteilung durchgeführt. Dies ist soweit kein problem. Nehmen wir nun an, dass wir die zwei primzahlen haben. Ihr fragt euch bestimmt warum ich p-1 gerechnet habe. Ganz einfach, jede teilfremde reste von der eulrischen Phi-Funktion einer Primzahl ist immer -1. Nehmen wir an, wir haben p = 5, somit sind die teilfremde reste 1,2,3,4. Haben wir p=4 , sind die teilfremde reste 1 und 3 = schwer zu berechnen. Deshalb spalten wir alles auf primzahlen auf. D.h (p-1) ist nichts anderes als phi(p).
zu beachten: "e" muss zu phi(n) teilfremd sein! e und N bilden dann logischerweise den "publickey".
Um die Inverse von e zu berechnen brauche ich jedoch noch k. Für das muss ich den erweiterten euklidischen Algorithmus anwenden. Genau damit habe ich probleme. Könnte mir jemand diesen Algorithmus erklären? Mit diesem Algorithmus kommt man dann auf den Private key sowie auf k.
Das problem bei diesem ganzen RSA-Knack-Algorithmus ist der punkt, indem man die Primzahlen sucht. Versucht mal von eienr 1024bit zahl die primzahlenteilung durchzuführen und ihr merkt was ich meine. Das ganze verhält sich nämlich exponentiel. Aber macht nichts, es ist eine nette herausfodering dies nachzuprogrammieren.
Nunja, da ich erst 16 jahre alt bin ist es sehr schwer für mich mit einem altersgenossen darüber zu diskutieren da dies meist über die Durchschnittsverhältnisse der jeweiligen Person geht und sie nur "bahnhof" verstehen. Darum versuche ich hier mein glück
Bisheriger Sourcecode:
Code:bool RSA::IsPrimzahl(__int64 nr) { for(__int64 d = 2; d*d <= nr; d++) { if (!(nr % d)) return false; } return true; } __int64 RSA::phiVonN(__int64 *pq) { return ((pq[0] -1) * (pq[1]-1)); } void RSA::Primzahlenzerlegen(__int64 Number, __int64* pq) { __int64 p; for(__int64 q = 3; (q*q) <= Number; q += 2) { if (Number % q == 0) { if (IsPrimzahl(q)) { p = Number / q; if (IsPrimzahl(p)) { pq[0] = p; pq[1] = q; break; } } } } }
Ergebnis 1 bis 4 von 4
Thema: RSA Kodierung
-
03.07.2009, 15:28 #1
 RSA Kodierung
RSA Kodierung
Geändert von aL1ien (03.07.2009 um 15:34 Uhr)
Tu peut t'le mettre dans l'cul.

-
03.07.2009, 17:25 #2

Die Primzahlen lassen sich trotz deiner sehr richtigen festellung das die prim-zerlegung ewig dauert bei großen zahlen (was ja der ganze trick is bei RSA) um einiges effizienter finden.
Guter Tipp dazu ist schonmal das Sieb des Atkin (http://en.wikipedia.org/wiki/Sieve_of_Atkin).
Hab vor einiger Teit mal sowas gebraucht (für Projekt Euler, falls das jmd was sagt) und das hier is dabei raus gekommen:
definitiv nicht der schönste code, aber für meinen zweck hats damals gereicht. Kann leider keine Garantie geben das er immer alle Primzahlen findet, weiß nur das es bei dem Fall auf den ich es anwenden musste geklappt hat.XML is like violence, if it doesn't fix the problem, you aren't using enough.
Random Numbers are too important to be left to chance.
-
03.07.2009, 18:07 #3

Hallo,
Ich danke dir erstmal für deine Antwort.
Ich habe hier mal ein paar Gedankengänge aufgeschrieben. Ich hoffe, dass man es erkennt. In dern schwarz umrandeten rechtecken findet man jeweils die endlösung.
im schwarzumrandeten teil steht: m * (m^k)^phi(n) = m
der rot gekennzeichnete ausdruck gibt IMMER 1 ( satz des eulers )
Nach reichlicher überlegen bin ich auch noch zu einer zweiten, bisher nicht publizierten lösung gekommen:
Im schwarzen bereich steht:
beispiel:
z5(ganze zahlen von 5) {1,2,3,4}
2*4 = 8 modulo 5 = 3 (jede multiplikation wird nicht grösser als 5 sein)
wie komme ich hier nun auf den Inhalt?
ganz einfach:
x^4 = 3
hier muss ich dann nurnoch einsetzen. Jedoch, was ist schneller? Soll ich jede erdenkliche methode durchprobieren oder wieder auf die erst genannte version zurückkommen?
Bitte nehmt euch zeit um versuchen zu verstehen was auf dem Papier steht, denn nur so versteht ihr schlussendlich wie ich dadrauf gekommen bin.
edit:// Ach ja, ich finde nicht das meine variante sehr lange dauert. Ich habe eine 64bit zahl in 0.5 - 1.5 secs in primzahlen aufgeteilt
Geändert von aL1ien (03.07.2009 um 18:45 Uhr)
Tu peut t'le mettre dans l'cul.

-
05.07.2009, 16:25 #4

So jetzt erklaer mir bitte nochmal genau was du willst du sprichst von RSA nachrpogrammieren und wenig speater vom knacken. Willst du eine RSA implemntation schreiben oder einen cracker ? Ausserdem ich kann beim besten Willen nicht genau erkennen was du da auf dem Papier geschrieben hast scans entweder in besserer qualitaet nochmal ein oder nochbesser schreibs in latex und haengs als pdf an.
MFGKnowledge is power - don't abuse it!
Fuer niveauvolle Anfragen bin ich unter 139156343 erreichbar
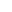

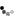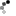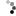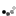
 Zitieren
Zitieren